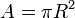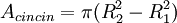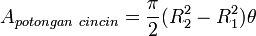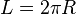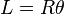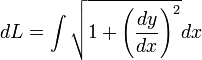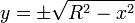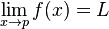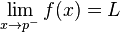1. Persamaan 2x2 - 2mx - 4x + 5m - 2 = 0
mempunyai dua akar nyata berbeda untuk
m =L
A. 2 < m < 4
B. 2 £ m £ 4
C. m £ 2 atau m £ 4
D. m < 2 atau m > 4
E. m £ -2 atau m ³ 4
2. Persamaan kuadrat 5x2 - 7x - 8 = 0
memiliki akar-akar a dan b . Persamaan
kuadrat baru yang akar-akarnya
2a
1
dan
2b
1
adalah ....
A. 32x2 +14x - 5 = 0
B. 32x2 -14x + 5 = 0
C. 3x2 -14x - 5 = 0
D. 8x2 +14x - 5 = 0
E. 8x2 -14x - 5 = 0
3. Dalam segitiga ABC berlaku
a2 = b2 + c2 - bc 3,maka sudut A = ....
A. 300
B. 450
C. 600
D. 1200
E. 1500
4. Nilai x yang memenuhi
22x - 3.2x+1 + 8 < 0 adalah ....
A. 1 < x < 2
B. -1 < x < 2
C. - 2 < x < 1
D. x > 2
E. x <1
5. Jika 2 log3 = a dan 2 log5 = b maka
5 log135 =L
A. ab + b
B. 3 + a-1b
C. a + ab
D. 1+ a-1b
E. 1+ 3ab-1
6. Jika
=
14 13
24 23
4 3
1 2
2 3
a b
maka
a + b =L
A. 1
B. 3
C. 5
D. 9
E. 12
7. Tiga bilangan membentuk barisan
aritmatika, bila suku ke-2 dikurangi 2
maka terbentuk barisan geometri dengan
r =2, jumlah ke-3 bilangan itu ....
A. 28
B. 30
C. 42
D. 48
E. 64
8. Jika
log x + log x2 +L+ log x20 = 210, maka
x yang memenuhi adalah ....
A. 0.1
B. 5
C. 10
D. 25
E. 100
9. Seorang siswa harus mengerjakan 5 soal
dari 7 soal yang tersedia dan soal no. 1
yang tersedia harus dikerjakan, maka
banyak pilihan yang dikerjakan =....
A. 6
B. 8
C. 10
D. 18
E. 20
10. Dalam sebuah kotak terdiri dari 10
jeruk dengan 4 buah jeruk busuk. Bila
diambil 3 secara acak, maka peluang
ketiganya baik adalah ....
A. 1/20
B. 1/10
C. 1/6
D. 3/20
E. 3/10
11. Jika , 3
2 6
3 4
( ) ¹
-
= + x
x
x
f x maka
f -1 (5) =L
A. -2
B. 2
C. 3
D. 4
E. 4.5
12. - - - =L
®¥
lim( x2 5x x 2)
x
A. 0
B. -4 ½
C. 4 ½
D. ½
E. ¥
Khoirotun Nisak 19 MATEMATIKA
Senin, 28 Oktober 2013
model matematika
Sistem pertidaksamaan linear yang telah dijelaskan sebelumnya dapat
diterapkan pada permasalahan sehari-hari dengan memodelkan
permasalahan tersebut ke dalam model matematika.
Sebagai ilustrasi perhatikan contoh berikut. PT. Samba Lababan
memproduksi ban motor dan ban sepeda. Proses pembuatan ban motor
melalui tiga mesin, yaitu 2 menit pada mesin I, 8 menit pada mesin II, dan
10 menit pada mesin III. Adapun ban sepeda diprosesnya melalui dua
mesin, yaitu 5 menit pada mesin I dan 4 menit pada mesin II. Tiap mesin
ini dapat dioperasikan 800 menit per hari. Untuk memperoleh keuntungan
maksimum, rencananya perusahaan ini akan mengambil keuntungan
Rp40.000,00 dari setiap penjualan ban motor dan Rp30.000,00 dari setiap
penjualan ban sepeda. Berdasarkan keuntungan yang ingin dicapai ini,
maka pihak perusahaan merencanakan banyak ban motor dan banyak
ban sepeda yang akan diproduksinya dengan merumuskan berbagai
kendala sebagai berikut.
Perusahaan tersebut memisalkan banyak ban motor yang diproduksi
sebagai x dan banyak ban sepeda yang diproduksi sebagai y, dengan x dan y
bilangan asli. Dengan menggunakan variabel x dan y tersebut, perusahaan
itu membuat rumusan kendala-kendala sebagai berikut.
Pada mesin I : 2x 5y 800 …. Persamaan 1
Pada mesin II : 8x 4y 800 .… Persamaan 2
Pada mesin III : 10 x 800 .… Persamaan 3
x, y bilangan asli : x 0, y 0 .… Persamaan 4
Fungsi tujuan (objektif) yang digunakan untuk memaksimumkan keuntungan
adalah f(x, y) 40.000x 30.000y. Dalam merumuskan masalah tersebut,
PT. Samba Lababan telah membuat model matematika dari suatu masalah
diterapkan pada permasalahan sehari-hari dengan memodelkan
permasalahan tersebut ke dalam model matematika.
Sebagai ilustrasi perhatikan contoh berikut. PT. Samba Lababan
memproduksi ban motor dan ban sepeda. Proses pembuatan ban motor
melalui tiga mesin, yaitu 2 menit pada mesin I, 8 menit pada mesin II, dan
10 menit pada mesin III. Adapun ban sepeda diprosesnya melalui dua
mesin, yaitu 5 menit pada mesin I dan 4 menit pada mesin II. Tiap mesin
ini dapat dioperasikan 800 menit per hari. Untuk memperoleh keuntungan
maksimum, rencananya perusahaan ini akan mengambil keuntungan
Rp40.000,00 dari setiap penjualan ban motor dan Rp30.000,00 dari setiap
penjualan ban sepeda. Berdasarkan keuntungan yang ingin dicapai ini,
maka pihak perusahaan merencanakan banyak ban motor dan banyak
ban sepeda yang akan diproduksinya dengan merumuskan berbagai
kendala sebagai berikut.
Perusahaan tersebut memisalkan banyak ban motor yang diproduksi
sebagai x dan banyak ban sepeda yang diproduksi sebagai y, dengan x dan y
bilangan asli. Dengan menggunakan variabel x dan y tersebut, perusahaan
itu membuat rumusan kendala-kendala sebagai berikut.
Pada mesin I : 2x 5y 800 …. Persamaan 1
Pada mesin II : 8x 4y 800 .… Persamaan 2
Pada mesin III : 10 x 800 .… Persamaan 3
x, y bilangan asli : x 0, y 0 .… Persamaan 4
Fungsi tujuan (objektif) yang digunakan untuk memaksimumkan keuntungan
adalah f(x, y) 40.000x 30.000y. Dalam merumuskan masalah tersebut,
PT. Samba Lababan telah membuat model matematika dari suatu masalah
integral tak tentu
1) Rumus-Rumus Integral Tak Tentu Fungsi Aljabar dan Trigonometri
1. ò dx = x + c
2. ò a dx = a ò dx = ax + c
3. ò xn dx = + c
4. ò sin ax dx = – cos ax + c
5. ò cos ax dx =sin ax + c
6. ò sec2 ax dx = tan ax + c
7. ò [ f(x) ± g(x) ] dx = ò f(x) dx ± ò g(x) dx
Catatan
1. Identitas trigonometri yang biasa digunakan
a. 2sinA×cosB = sin(A + B) + sin(A – B)
b. –2sinA×sinB = cos(A + B) – cos(A – B)
c. sin2A =
d. cos2A =
e. sin 2A = 2sin A × cos A
2. Teknik Penyelesain Bentuk Integran
Misalkan u(x) dan v(x) masing-masing adalah fungsi dalam variabel x, maka metode pengintegralan yang bisa digunakan adalah:
a. Metode substitusi
Jika bentuk integran : ò u v dx , dengan u dan v memiliki hubungan, yaitu v dx = du
b. Metode Parsial dengan TANZALIN
Jika bentuk integran : ò u dv , dengan u dan v tidak memiliki hubungan, yaitu v dx ≠ du
Senin, 30 September 2013
persamaan lingkaran
Suatu lingkaran memiliki persamaan
 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan 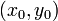 adalah koordinat pusat lingkaran.
adalah koordinat pusat lingkaran.
 dan jari-jari luar
dan jari-jari luar 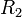 .
.

Luas lingkaran dapat dihitung dengan memotong-motongnya sebagai elemen-elemen dari suatu juring untuk kemudian disusun ulang menjadi sebuah persegi panjang yang luasnya dapat dengan mudah dihitung. Dalam gambar r berarti sama dengan R yaitu jari-jari lingkaran.
 dan jari-jari luar
dan jari-jari luar 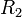 , yaitu
, yaitu
 rumus ini kembali menjadi rumus luas lingkaran.
rumus ini kembali menjadi rumus luas lingkaran.
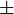 mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan 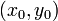 adalah koordinat pusat lingkaran.
adalah koordinat pusat lingkaran.Persamaan parametrik
Lingkaran dapat pula dirumuskan dalam suatu persamaan parameterik, yaituLuas lingkaran
Luas lingkaran memiliki rumus dan jari-jari luar
dan jari-jari luar 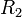 .
.Penjumlahan elemen juring

Luas lingkaran dapat dihitung dengan memotong-motongnya sebagai elemen-elemen dari suatu juring untuk kemudian disusun ulang menjadi sebuah persegi panjang yang luasnya dapat dengan mudah dihitung. Dalam gambar r berarti sama dengan R yaitu jari-jari lingkaran.
[sunting]Luas juring
Luas juring suatu lingkaran dapat dihitung apabila luas lingkaran dijadikan fungsi dari R dan θ, yaitu;Luas cincin lingkaran
Suatu cincin lingkaran memiliki luas yang bergantung pada jari-jari dalam dan jari-jari luar
dan jari-jari luar 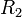 , yaitu
, yaitu rumus ini kembali menjadi rumus luas lingkaran.
rumus ini kembali menjadi rumus luas lingkaran.Luas potongan cincin lingkaran
Dengan menggabungkan kedua rumus sebelumnya, dapat diperolehKeliling lingkaran
Keliling lingkaran memiliki rumus:Panjang busur lingkaran
Panjang busur suatu lingkaran dapat dihitung dengan menggunakan rumus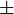 mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.]Pi atau π
Nilai pi adalah suatu besaran yang merupakan sifat khusus dari lingkaran, yaitu perbandingan dari keliling K dengan diameternya D:
- SILAHKAN KLIK DISINI!!!!!
- power point lingkaran lingkaran
lingkaran
Elemen-elemen suatu lingkaran.
Dalam geometri Euklid, sebuah lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu, yang disebut jari-jari, dari suatu titik tertentu, yang disebutpusat. Lingkaran adalah contoh dari kurva tertutup sederhana, membagi bidang menjadi bagian dalam dan bagian luar.
Dalam geometri Euklid, sebuah lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu, yang disebut jari-jari, dari suatu titik tertentu, yang disebutpusat. Lingkaran adalah contoh dari kurva tertutup sederhana, membagi bidang menjadi bagian dalam dan bagian luar.
Elemen lingkaran
Elemen-elemen yang terdapat pada lingkaran, yaitu sbb:- n sebuah titik di dalam lingkaran yang menjadi acuan untuk
menentukan jarak terhadap himpunan titik yang membangun lingkaran
sehingga sama. Elemen lngkiaran yang berupa titik, yaitu :
- Titik pusat (P)
merupakan jarak antara titik pusat dengan lingkaran harganya konstan dan disebut jari-jari.
- Titik pusat (P)
- Elemen lingkaran yang berupa garisan, yaitu :
- Jari-jari (R)
merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran. - Tali busur (TB)
merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda (TB). - Busur (B)
merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran. - Keliling lingkaran (K)
merupakan busur terpanjang pada lingkaran. - Diameter (D)
merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas. - Apotema
merupakan garis terpendek antara tali busur dan pusat lingkaran.
- Jari-jari (R)
- Elemen lingkaran yang berupa luasan, yaitu :
- Juring (J)
merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya. - Tembereng (T)
merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya. - Cakram (C)
merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.
- Juring (J)
limit fungsi
Fungsi pada garis bilangan riil
Bila f : R R terdefinisi pada garis bilangan riil, dan p, L
R terdefinisi pada garis bilangan riil, dan p, L  R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:
R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:Limit searah
Masukan x dapat mendekati p dari atas (kanan di garis bilangan) atau dari bawah (kiri). Dalam hal ini limit masing-masingnya dapat ditulis sebagaiDefinisi formal adalah sebagai berikut. Limit f(x) saat x mendekati p dari atas adalah L bila, untuk setiap ε > 0, terdapat sebuah bilangan δ > 0 sedemikian rupa sehingga |f(x) – L| < ε pada saat 0 < x – p < δ. Limit f(x) saat x mendekati p dari bawah adalah L bila, untuk setiap ε > 0, terdapat bilangan δ > 0 sehingga |f(x) – L| < ε bilamana 0 < p – x < δ.
Bila limitnya tidak ada terdapat osilasi matematis tidak nol.
Turunan.
Dalam matematika, turunan dari suatu fungsi adalah satu dari dua konsep utama dalam kalkulus. Invers dari turunan disebut antiturunan atau integral tak tentu.
- y‘ adalah simbol untuk turunan pertama.
- y” adalah simbol untuk turunan kedua.
- y”’ adalah simbol untuk turunan ketiga.
 dan
dan  adalah
adalah 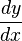 dan
dan 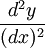
Langganan:
Komentar (Atom)